What is happens when you cant the rifle is the following:

To make my calculations easier to understand for everyone I assume that when I cant the rifle I cant around the axis of the bore, so bore is the center of rotation. To make it even clearer I take some exaggerated scope heights, so 2 cm above bore and 10 cm above the bore. For the rifle cant I take 5 degrees and for the distance I'm using 50 meters (which is also the initial zeroing distance). I'm using metric units because that's easier for me to use.
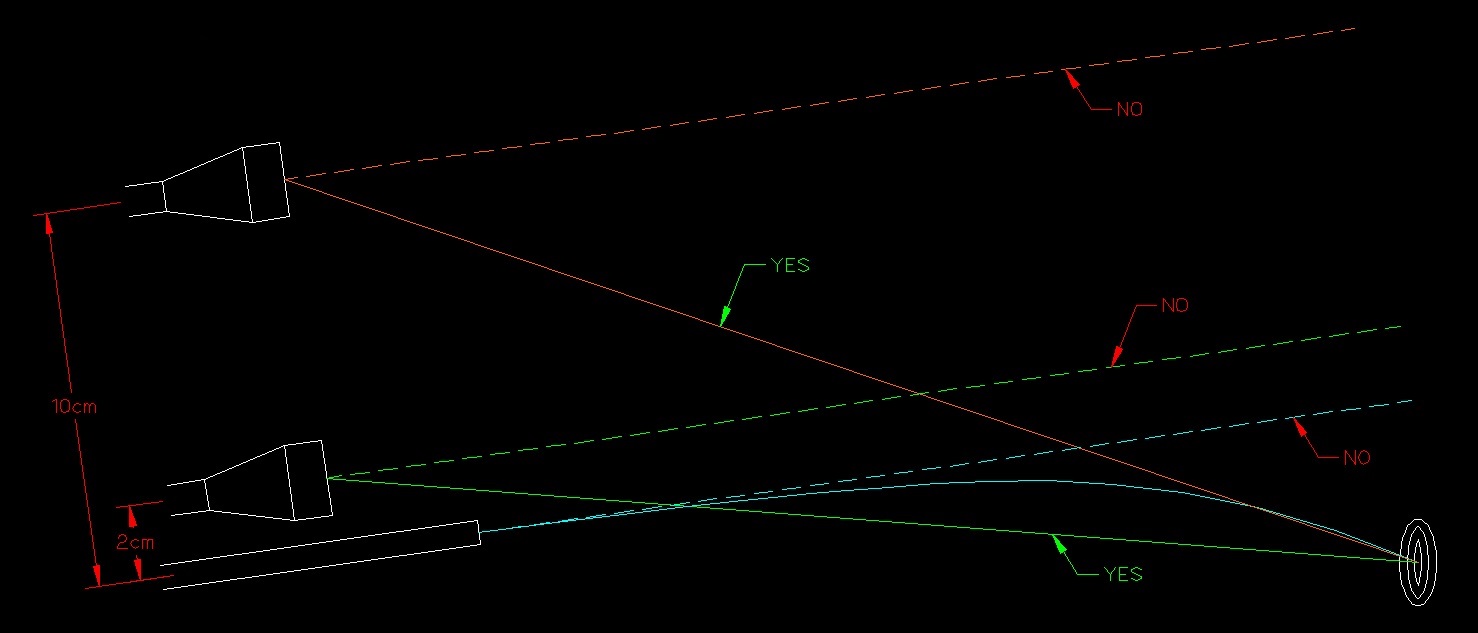
When I start canting my rifle the following thing happens to the alignment of the bore and scope:

The black dot is the center of the bore, the green dot is the scope placed at 2cm and the orange dot is the scope placed at 10 cm. The purple line is the new height of the scope above the bore (vertical) and the red line is the new horizontal misalignment of the bore.
The purple line can be calculated with the following formula:
height above bore * cos (canted angle) The red line can be calculated with the following formula:
height above bore * sin (canted angle) So for our two different scope heights:
2 cm with 5 degree cant ->
new vertical distance (purple line) becomes 1.99 cm and the horizontal distance (red line) becomes 0.17 cm 10 cm with 5 degree cant ->
vertical becomes 9.96 cm and horizontal 0.87 cm For the next calculation I'm using the scope as center of rotation since your aiming at a fixed point, the calculated values above stay the same but we then assume the bore swivels under the center of the scope.

As you can see the horizontal misalignment will be magnified when increasing the distance. Now using chairgun I determine the first crossing point with the trajectory for both scope heights:
1.99 cm ->
first crossing point is 5,5 meters 9.96 cm ->
first crossing point is 15.8 meters To calculate the misalignment on target the following is used:
2 cm ->
0.17 / 5.5 * (50 - 5.5) = 1.375 cm 10 cm ->
0.87 / 15.8 * (50 - 15.8) = 1.88 cm As you can see the black line is longer than the green line (use Pythagoras and you'll see), on a very long distance the actual flight distance is longer than the sight distance which causes an extra vertical drop due to the bullet/pellet trajectory. For pellet ranges this is can be neglected.
With keeping the same 50 meter zeroing distance and shooting at 100 meters the error will grow linearly:
2 cm ->
0.17 / 5.5 * (100 - 5.5 ) = 2.92 cm 10 cm ->
0.87 / 15.8 * (100 - 15.8) = 4.64 cm So to conclude some things that are debated above:
- gravity/trajectory doesn't come in to play at airgun distances (calculate the new flight distance vs uncanted flight distance and you'll see the extra distance is below 0.0001 %). If the extra distance would matter a higher placed scope will give less drop. Check chairgun for this, place you scope on two different heights and check at 100 meters, lets say 1 % extra due to cant will make the actual distance 101 meters. A higher placed scope will have less drop on the 1 meter extra than a lower placed scope.
- yes it already matters at the zeroing distance
- Larger canting errors/angles makes it worse
- Longer distance makes it worse
- Scope mounted higher above the bore makes it worse