One discussion sticking point seems to be some "either or" concept of pellet stabilization as being the consequence of either rifling twist rate , or pellet spin rate (rpm).
To be clear, gyroscopic stability is the result of gyroscopic torque.
Gyroscopic torque = Angular momentum x Angular velocity.
Both on the right side of the equation, depend upon RPM.
So we cannot discuss the fraction of projectile stability that depends upon spin, without discussing RPM (angular velocity) of the pellet/bullet. We cannot afford to get the rifling twist rate and pellet spin per unit of distance travelled confused with the true spin rate of the projectile which is its spin rate per unit of time viz., RPM.
RPM is derived from rifling twist rate AND projectile velocity. AZ has given an example but I feel has failed to point out that the actual stability rating of the example with 36,000 RPM will not be the same as that with 18,000 RPM even though they both have the same number of spins per unit distance derived from the rifling twist rate.
Rifling/barrel twist rate and the spin imposed on the projectile per unit of travel, is not by itself the stabilizing influence. That twist rate must be matched to projectile velocity in order to produce the stabilizing gyroscopic torque which is designed to keep the projectile orientated in space; and to reduce the possibility of precession and in the case of bullets, from tumbling.
So, as I implied in introduction, stabilization of any given weight, diameter and length of pellet depends on the interaction of both twist rate and ACTUAL spin rate RPM.
One common misconception, which has also appeared here, is that the spin per unit of travel imposed by twist rate is constant throughout flight. It is not.
It is well known that radial velocity decays more slowly than linear velocity when compared to the initial states.
The outcome is that down range the number of rotations per unit of travel actually increases as though the "twist rate" has become faster whilst RPM is still decaying. This changes the relationship between the velocity and the effective "twist rate". So what may have begun as a well matched projectile to its gyro torque then may become less than optimal; and the stability may subsequently suffer. ... At that point, as Alan implied somewhere, the earlier stable projectile may become de- stabilized and in my son's terms (when he handed me the controls in an F111 simulator) it "Goes to God".
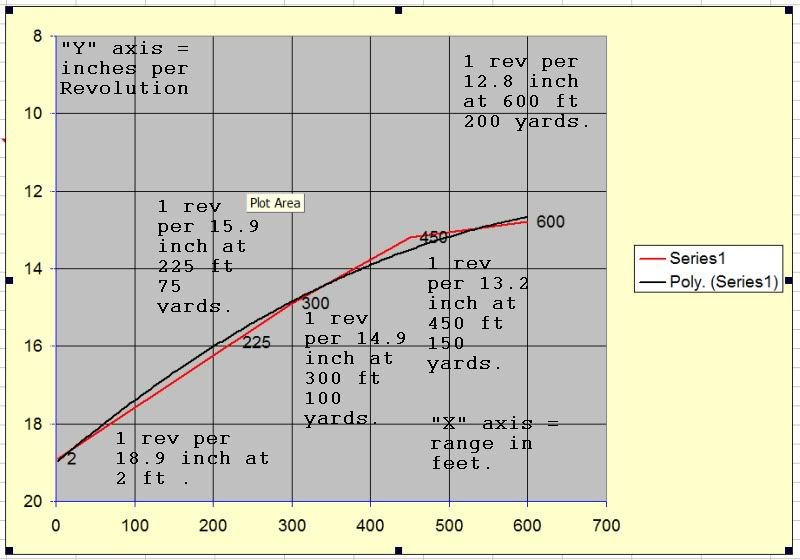
Here is some data from a test I did some years ago to establish what happened to a .25 cal JSB King pellet Revolution rate per unit distance (effective twist rate).
Result data points inserted were:
2 ft = 1 rev per 18.9 inches ie., 1:18.9 (assumed to equal rifling twist rate of the BSA 0.25 cal barrel).
So:
2 feet = 1: 18.9
225 feet/ 75 yards = 1:15.9
300 feet/ 100 yards = 1:14.9
450 feet/ 150 yards = 1:13.2
600 feet/ 200 yards = 1:12.8
Graph :
200 yd double target as example of data collection:

Example of two target angles rotation change from the two screens, Pellets were marked to show radial displacement through the screens.:

I hope this is found to be helpful within the context of the discussion.
Best regards, Harry.


