Could someone please explain exactly what "Standard Deviation" is and how important it is when chronographing pellets.
What is standard deviation?
- Thread starter Doug
- Start date
"SD" is the average difference in feet per second between shots.
My 2¢...
I, personally, put a lot of focus on the SD of a rifle's shot string because it shows me how consistent that rifle is. Consistency = less variation = repeatability = accuracy.
Now there are MANY variables that go into putting multiple pellets in the same hole and this is just one piece of that puzzle.
Tom
My 2¢...
I, personally, put a lot of focus on the SD of a rifle's shot string because it shows me how consistent that rifle is. Consistency = less variation = repeatability = accuracy.
Now there are MANY variables that go into putting multiple pellets in the same hole and this is just one piece of that puzzle.
Tom
Upvote 0
Hay Doug
Standard Deviation (STD) is in essence the quality of your data, a high # is means your data has a high variance, and the closer you get to zero, the more precise your data.
It is an important number, but if you look at your fps spread, than you do not need to concern yourself with it as much, especially since a lot of shooters tend to speak in terms of velocity spread.
Make sense?
Standard Deviation (STD) is in essence the quality of your data, a high # is means your data has a high variance, and the closer you get to zero, the more precise your data.
It is an important number, but if you look at your fps spread, than you do not need to concern yourself with it as much, especially since a lot of shooters tend to speak in terms of velocity spread.
Make sense?
Upvote 0
Standard deviation is a statistical term. It is derived mathematically (yeah, like I really understand this stuff). My last statistics class was in 1982, so a very long time ago.
take a look at this Wiki page for an explanation:
https://en.wikipedia.org/wiki/Standard_deviation
For air gunning (and folks please correct me if I'm wrong), when you do, for example, a shot string of 10 or 20 shots, and if the standard deviation is small, that means the gun is sending the pellets down the barrel with consistent energy between shots. the smaller the Standard Deviation, the more consistent the gun is delivering air and energy to the pellet. Consistency between shots translates to more consistent accuracy.
If the standard deviation is large, then the gun is inconsistent, and probably won't be as accurate as a gun with a small standard deviation. One shot will be perfect, but because the gun delivers a different amount of air / energy to the next pellet, it'll land somewhere completely different.
Let me know if that made sense, if it did, I'll be as surprised as the next person.
take a look at this Wiki page for an explanation:
https://en.wikipedia.org/wiki/Standard_deviation
For air gunning (and folks please correct me if I'm wrong), when you do, for example, a shot string of 10 or 20 shots, and if the standard deviation is small, that means the gun is sending the pellets down the barrel with consistent energy between shots. the smaller the Standard Deviation, the more consistent the gun is delivering air and energy to the pellet. Consistency between shots translates to more consistent accuracy.
If the standard deviation is large, then the gun is inconsistent, and probably won't be as accurate as a gun with a small standard deviation. One shot will be perfect, but because the gun delivers a different amount of air / energy to the next pellet, it'll land somewhere completely different.
Let me know if that made sense, if it did, I'll be as surprised as the next person.
Upvote 0
Doug, I am not a airgun expert, but do have a lot of experience in the pro side of serious PB competition. "STD" can only be of any value if your projectiles be it pellets or bullets have a consistent coefficient. Meaning, weight and shape, so to get a good "STD" with an air rifle I would weigh my pellets and definitely use a quality match grade version. That would show if your gun is giving a good or bad velocity spread aka "STD". I have found a big deviation in pellet coefficients by just weighing them, it was surprising how much they could vary. Hope this helps brother. Dale
Upvote 0
The same question came to my mind just a couple of days ago. I've always looked at ES which was easier to calculate. I shot a 10 shot string through my chronograph and played with the results as calculated by the chronograph. It was actually the first time in 5 years that I actually did that. I think everyone's answer is correct but if you want to calculate it on paper I believe this is how. I could be wrong and I don't mind being enlightened..
Shot # Vel. Diff
1 887
2 891 4
3 886 5
4 886 0
5 893 7
6 885 8
7 881 4
8 881 0
9 890 9
10 888 2
Sum of differences is 39 divided by 9 shots is 4,3 Averaged Deviation. (I think)
Extreme spread is 10
Shot # Vel. Diff
1 887
2 891 4
3 886 5
4 886 0
5 893 7
6 885 8
7 881 4
8 881 0
9 890 9
10 888 2
Sum of differences is 39 divided by 9 shots is 4,3 Averaged Deviation. (I think)
Extreme spread is 10
Upvote 0
+\- one standard deviation means approximately 67% of a population (shot string in this case) will be within that value. So for example, a 100 shot string with a standard deviation of 20 fps will have roughly 33 shots greater than 20 fps from the population average. Standard deviation is a simple statistical calculation, but in my opinion is not as helpful as extreme spread. Most guys want to know the total shot variation to achieve the best possible accuracy and this comes from extreme spread.
Upvote 0
Thanks you all for helping me to understand this. As an example I entered a 10 shot string into the J.C. Brown & Werner Wicha spreadsheet and got this:
1 960 Min. 955
2 958 Max 961
3 956 Avg 958
4 956 ES 6
5 961 SD 2.31
6 961 Avg '# 51.75
7 955
8 956
9 957
10 960
Using jking's example above I came up with a total difference between shots of 20, divided by 9, and got a SD of 2.2. It's close but I'm unsure if it is the correct math formula or not.
1 960 Min. 955
2 958 Max 961
3 956 Avg 958
4 956 ES 6
5 961 SD 2.31
6 961 Avg '# 51.75
7 955
8 956
9 957
10 960
Using jking's example above I came up with a total difference between shots of 20, divided by 9, and got a SD of 2.2. It's close but I'm unsure if it is the correct math formula or not.
Upvote 0
Standard deviation is the square root of the variance. Variance is the average of of squared difference from the mean (average) of all your data. The calculation changes slightly if the data is a sample of a total population, but in this instance you are calculating the entire population (your 10 shot string)
This link has a pretty good explanation of SD, variance and the calculations for both
http://www.mathsisfun.com/data/standard-deviation.html
This link has a pretty good explanation of SD, variance and the calculations for both
http://www.mathsisfun.com/data/standard-deviation.html
Upvote 0
I would think SD value is more important then ES because if you have 50 shots with a low SD but have a high ES, your gun is shooting very consistent but you might get one shot that will throw your ES way off.
That one shot might be due to a bad pellet or some other reason but the other 49 shots were very consistent which will be your ES.
Having a low ES and a low SD is something we all try to achieve.
That one shot might be due to a bad pellet or some other reason but the other 49 shots were very consistent which will be your ES.
Having a low ES and a low SD is something we all try to achieve.
Upvote 0
Upvote 0
Good information in here. All I need now is a chronograph... Although my rifle is pretty accurate I still would like to know more about the fps and get out to further shots. Thanks guys!
Upvote 0
SD is one of the most valuable pieces of information that you can get from the chrony. It's nice to know both SD and ES. But I usually ignore the ES, as SD tells me a lot more.
Example:
Assume two 10-shot strings.
10 shot string #1:
ES=44fps
SD=14fps
Average=800fps
10 shot string #2:
ES=40fps
SD=20fps
Average=800fps
SD is a better indicator of shot string quality and hit probability.
If shooting a difficult field target, a gun yielding string #1 will likely give a much higher target hit rate than a gun yielding string #2. That is an extreme example, but it still holds for examples with lower ES and lower SD.
Example:
Assume two 10-shot strings.
10 shot string #1:
ES=44fps
SD=14fps
Average=800fps
10 shot string #2:
ES=40fps
SD=20fps
Average=800fps
SD is a better indicator of shot string quality and hit probability.
If shooting a difficult field target, a gun yielding string #1 will likely give a much higher target hit rate than a gun yielding string #2. That is an extreme example, but it still holds for examples with lower ES and lower SD.
Upvote 0
Example shot string #2 is a great but certainly extreme example, the shots are either 820 fps or 780 fps with nothing in between. Stats are not necessary to realize that is a highly undesirable situation. I'd think watching the real time crony feedback would raise a red flag.
Upvote 0
G
Guest
Guest
Scotchmo is right on his point. All other things being equal I'd take a gun shooting an SD of 1 over an SD of 2 no matter what the ES was. ES has no predictive value unless you shoot lots of strings and do analysis based upon a number of measurements. SD is intended to be predictive. A gun might show a good SD for ten strings and an exceptionally bad ES in one of those ten strings. It is much less likely that a gun will show one bad SD out of a set of 10 strings. Another way to say that is that 1 shot in a hundred can drive your ES into the ugly zone but it takes a LOT of bad shots to push one SD into the ugly zone.
Just my two...
Upvote 0
oldspook -
I'm glad you responded & you are right
. Standard deviation is a good predictive calculation that is intended to represent the total population of a normal distribution. Scotchmo's string #2 is not a normal distribution - I suspect he knows this. However, it is a very clever & extreme example where standard deviation provided what appears to be better information versus ES.
As always, I need to be more clear in my writing. I prefer ES for a gun that I have verified has a normal distribution. Flyers will happen and influence ES - your point is accurate & conceded.
Now I'm no expert on the varying shot string characteristics of the PCP airgun world, but I do know (as most member do) MV is important for accuracy - especially as target distance increases. So, if one has a gun that shots a normal distribution & longer range accuracy is important, what statistical measure would you put more priority on?
Your answer may vary with regulated versus un-regulated airguns, but please think about it in terms of user refill pressure. What I mean is that most guys refill a PCP at some fixed air tube pressure. Looking forward to your response.
I'm glad you responded & you are right
. Standard deviation is a good predictive calculation that is intended to represent the total population of a normal distribution. Scotchmo's string #2 is not a normal distribution - I suspect he knows this. However, it is a very clever & extreme example where standard deviation provided what appears to be better information versus ES.As always, I need to be more clear in my writing. I prefer ES for a gun that I have verified has a normal distribution. Flyers will happen and influence ES - your point is accurate & conceded.
Now I'm no expert on the varying shot string characteristics of the PCP airgun world, but I do know (as most member do) MV is important for accuracy - especially as target distance increases. So, if one has a gun that shots a normal distribution & longer range accuracy is important, what statistical measure would you put more priority on?
Your answer may vary with regulated versus un-regulated airguns, but please think about it in terms of user refill pressure. What I mean is that most guys refill a PCP at some fixed air tube pressure. Looking forward to your response.
Upvote 0
Good explanations so far.... my take cause I like stats
you can have averages. Suppose your gun should is shooting an average of 880 FPS. That sounds pretty good. You can have that average if you have lots of shots at 1300 FPS and lots at 400 FPS. Standard deviation is a way to express how far shots deviant from the mean. The lower the SD the closer every shot (or whatever) is to the mean. Lower numbers mean most shots are about the same speed.
SD involves lots of finding means and squaring, but in a nutshell SD means consistency. Low numbers = high consistency.
you can have averages. Suppose your gun should is shooting an average of 880 FPS. That sounds pretty good. You can have that average if you have lots of shots at 1300 FPS and lots at 400 FPS. Standard deviation is a way to express how far shots deviant from the mean. The lower the SD the closer every shot (or whatever) is to the mean. Lower numbers mean most shots are about the same speed.
SD involves lots of finding means and squaring, but in a nutshell SD means consistency. Low numbers = high consistency.
Upvote 0
G
Guest
Guest
Clearly you know your maths. Well written. And yes scotchmo did give a well contrived (and for sure nearly impossible) counter example."parallax"oldspook -
I'm glad you responded & you are right
As always, I need to be more clear in my writing. I prefer ES for a gun that I have verified has a normal distribution. Flyers will happen and influence ES - your point is accurate & conceded.
Now I'm no expert on the varying shot string characteristics of the PCP airgun world, but I do know (as most member do) MV is important for accuracy - especially as target distance increases. So, if one has a gun that shots a normal distribution & longer range accuracy is important, what statistical measure would you put more priority on?
Your answer may vary with regulated versus un-regulated airguns, but please think about it in terms of user refill pressure. What I mean is that most guys refill a PCP at some fixed air tube pressure. Looking forward to your response.
Whether regulated or unregulated, springer, or multi-pump, if a gun is shooting a normal distribution then the SD is the predictive value you want to place weight upon. This is because the extreme shot is not predictable. It could occur now or at the end of the string. With SD you at least know that 2/3 of your shots will fall withing one SD of the average velocity. Additionally if that is not sufficiently accurate and you require more precision to hunt humanely, then you limit your range based upon some fraction of the SD which will give you the probability of a hit that you require. So for example if the SD told me that 2/3 of my shots would fall within 12 fps of the average and that wasn't good enough I could use the acceptable probability of a hit, say 95%, to estimate the ES that I would have to accept. That ES would be the ES which could be calculated from the chart here:
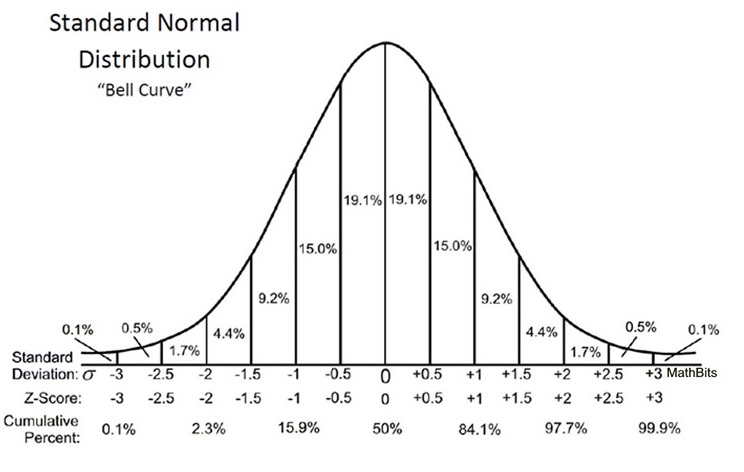
From that we can see that the ES we would have to accept would be +/- 2 standard deviations from the mean (we wanted 95%). In our case we would be limited to shooting at our target from ranges where an ES of less than 48 fps would hit the target (our example was SD=12 fps). Plus or minus 2 standard deviations is plus or minus (2*12) for our example.
Some folks would say that only a 100% probability of a hit is acceptable and so we should consider the ES to be the determining factor. The ES is a property of the string it represents and is statistically less significant than the SD because it is composed of only 2 samples in the sample set. If you use the ES of one string, the next string you shoot will almost certainly have a different ES, it might be larger or smaller but because it is only 2 samples from the sample set it will vary more widely than the Standard Deviation from set to set. So you would probably need to shoot a large number of strings to find out what your true maximum ES was... and then you would be into doing the Standard Deviation of your Extreme Spread... probably more pain than gain at that point.
I want to add this; there is a possibility that the ES of one string falls outside the ES of another string and you can actually compute that probability using the Standard Deviation as the basis of the calculation. In our example (SD = 12); The probability of a shot being 36 feet faster than the average is 0.1% (1 in 1000). The probability of a shot being 36 feet slower than the average is 0.1%(1 in 1000). The probability of an ES of 72 fps is 0.01%(1 in 10000). All of this can be read directly from that graph, so nobody has to do that math again.
Upvote 0